Last update: April 16, 2024  Original

Integer factorization

In this article we list several algorithms for the factorization of integers, each of which can be either fast or varying levels of slow depending on their input.

Notice, if the number that you want to factorize is actually a prime number, most of the algorithms will run very slowly. This is especially true for Fermat's, Pollard's p-1 and Pollard's rho factorization algorithms. Therefore, it makes the most sense to perform a probabilistic (or a fast deterministic) primality test before trying to factorize the number.

Trial division

This is the most basic algorithm to find a prime factorization.

We divide by each possible divisor   $d$ . It can be observed that it is impossible for all prime factors of a composite number   $n$  to be bigger than   $\sqrt{n}$ . Therefore, we only need to test the divisors   $2\le d\le \sqrt{n}$ , which gives us the prime factorization in   $O(\sqrt{n})$ . (This is pseudo-polynomial time, i.e. polynomial in the value of the input but exponential in the number of bits of the input.)

The smallest divisor must be a prime number. We remove the factored number, and continue the process. If we cannot find any divisor in the range   $[2;\sqrt{n}]$ , then the number itself has to be prime.

vector<long long> trial_division1(long long n) {
    vector<long long> factorization;
    for (long long d = 2; d * d <= n; d++) {
        while (n % d == 0) {
            factorization.push_back(d);
            n /= d;
        }
    }
    if (n > 1)
        factorization.push_back(n);
    return factorization;
}

Wheel factorization

This is an optimization of the trial division. Once we know that the number is not divisible by 2, we don't need to check other even numbers. This leaves us with only   $50\mathrm{\%}$  of the numbers to check. After factoring out 2, and getting an odd number, we can simply start with 3 and only count other odd numbers.

vector<long long> trial_division2(long long n) {
    vector<long long> factorization;
    while (n % 2 == 0) {
        factorization.push_back(2);
        n /= 2;
    }
    for (long long d = 3; d * d <= n; d += 2) {
        while (n % d == 0) {
            factorization.push_back(d);
            n /= d;
        }
    }
    if (n > 1)
        factorization.push_back(n);
    return factorization;
}

This method can be extended further. If the number is not divisible by 3, we can also ignore all other multiples of 3 in the future computations. So we only need to check the numbers   $5,7,11,13,17,19,23,\dots$ . We can observe a pattern of these remaining numbers. We need to check all numbers with   $dmod6=1$  and   $dmod6=5$ . So this leaves us with only   $33.3\mathrm{\%}$  percent of the numbers to check. We can implement this by factoring out the primes 2 and 3 first, after which we start with 5 and only count remainders   $1$  and   $5$  modulo   $6$ .

Here is an implementation for the prime number 2, 3 and 5. It is convenient to store the skipping strides in an array.

vector<long long> trial_division3(long long n) {
    vector<long long> factorization;
    for (int d : {2, 3, 5}) {
        while (n % d == 0) {
            factorization.push_back(d);
            n /= d;
        }
    }
    static array<int, 8> increments = {4, 2, 4, 2, 4, 6, 2, 6};
    int i = 0;
    for (long long d = 7; d * d <= n; d += increments[i++]) {
        while (n % d == 0) {
            factorization.push_back(d);
            n /= d;
        }
        if (i == 8)
            i = 0;
    }
    if (n > 1)
        factorization.push_back(n);
    return factorization;
}

If we continue exending this method to include even more primes, better percentages can be reached, but the skip lists will become larger.

Precomputed primes

Extending the wheel factorization method indefinitely, we will only be left with prime numbers to check. A good way of checking this is to precompute all prime numbers with the Sieve of Eratosthenes until   $\sqrt{n}$ , and test them individually.

vector<long long> primes;

vector<long long> trial_division4(long long n) {
    vector<long long> factorization;
    for (long long d : primes) {
        if (d * d > n)
            break;
        while (n % d == 0) {
            factorization.push_back(d);
            n /= d;
        }
    }
    if (n > 1)
        factorization.push_back(n);
    return factorization;
}

Fermat's factorization method

We can write an odd composite number   $n=p\cdot q$  as the difference of two squares   $n=a^2-b^2$ :

  $$n={\left(\frac{p+q}{2}\right)}^2-{\left(\frac{p-q}{2}\right)}^2$$ 

Fermat's factorization method tries to exploit this fact by guessing the first square   $a^2$ , and checking if the remaining part,   $b^2=a^2-n$ , is also a square number. If it is, then we have found the factors   $a-b$  and   $a+b$  of   $n$ .

int fermat(int n) {
    int a = ceil(sqrt(n));
    int b2 = a*a - n;
    int b = round(sqrt(b2));
    while (b * b != b2) {
        a = a + 1;
        b2 = a*a - n;
        b = round(sqrt(b2));
    }
    return a - b;
}

This factorization method can be very fast if the difference between the two factors   $p$  and   $q$  is small. The algorithm runs in   $O(|p-q|)$  time. In practice though, this method is rarely used. Once factors become further apart, it is extremely slow.

However, there are still a large number of optimization options regarding this approach. By looking at the squares   $a^2$  modulo a fixed small number, it can be observed that certain values   $a$  don't have to be viewed, since they cannot produce a square number   $a^2-n$ .

Pollard's   $p-1$  method

It is very likely that at least one factor of a number is   $B$ -powersmooth for small   $B$ .   $B$ -powersmooth means that every prime power   $d^k$  that divides   $p-1$  is at most   $B$ . E.g. the prime factorization of   $4817191$  is   $1303\cdot 3697$ . And the factors are   $31$ -powersmooth and   $16$ -powersmooth respectably, because   $1303-1=2\cdot 3\cdot 7\cdot 31$  and   $3697-1=2^4\cdot 3\cdot 7\cdot 11$ . In 1974 John Pollard invented a method to extracts   $B$ -powersmooth factors from a composite number.

The idea comes from Fermat's little theorem. Let a factorization of   $n$  be   $n=p\cdot q$ . It says that if   $a$  is coprime to   $p$ , the following statement holds:

  $$a^{p-1}\equiv 1(\mathrm{mod}p)$$ 

This also means that

  $${\left(a^{(p-1)}\right)}^k\equiv a^{k\cdot (p-1)}\equiv 1(\mathrm{mod}p).$$ 

So for any   $M$  with   $p-1|M$  we know that   $a^M\equiv 1$ . This means that   $a^M-1=p\cdot r$ , and because of that also   $p|gcd(a^M-1,n)$ .

Therefore, if   $p-1$  for a factor   $p$  of   $n$  divides   $M$ , we can extract a factor using Euclid's algorithm.

It is clear, that the smallest   $M$  that is a multiple of every   $B$ -powersmooth number is   $\text{lcm}(1,2,3,4,\dots ,B)$ . Or alternatively:

  $$M=\prod _{\text{prime }q\le B}{q}^{\lfloor {\log }_{q}B\rfloor }$$ 

Notice, if   $p-1$  divides   $M$  for all prime factors   $p$  of   $n$ , then   $gcd(a^M-1,n)$  will just be   $n$ . In this case we don't receive a factor. Therefore, we will try to perform the   $gcd$  multiple times, while we compute   $M$ .

Some composite numbers don't have   $B$ -powersmooth factors for small   $B$ . For example, the factors of the composite number   $100000000000000493=763013\cdot 131059365961$  are   $190753$ -powersmooth and   $1092161383$ -powersmooth. We will have to choose   $B>=190753$  to factorize the number.

In the following implementation we start with   $B=10$  and increase   $B$  after each each iteration.

long long pollards_p_minus_1(long long n) {
    int B = 10;
    long long g = 1;
    while (B <= 1000000 && g < n) {
        long long a = 2 + rand() %  (n - 3);
        g = gcd(a, n);
        if (g > 1)
            return g;

        // compute a^M
        for (int p : primes) {
            if (p >= B)
                continue;
            long long p_power = 1;
            while (p_power * p <= B)
                p_power *= p;
            a = power(a, p_power, n);

            g = gcd(a - 1, n);
            if (g > 1 && g < n)
                return g;
        }
        B *= 2;
    }
    return 1;
}

Observe that this is a probabilistic algorithm. A consequence of this is that there is a possibility of the algorithm being unable to find a factor at all.

The complexity is   $O(B\log B{\log }^{2}n)$  per iteration.

Pollard's rho algorithm

Pollard's Rho Algorithm is yet another factorization algorithm from John Pollard.

Let the prime factorization of a number be   $n=pq$ . The algorithm looks at a pseudo-random sequence   $\{x_i\}=\{x_0,f(x_0),f(f(x_0)),\dots \}$  where   $f$  is a polynomial function, usually   $f(x)=(x^2+c)modn$  is chosen with   $c=1$ .

In this instance, we are not interested in the sequence   $\{x_i\}$ . We are more interested in the sequence   $\{x_{i}modp\}$ . Since   $f$  is a polynomial function, and all the values are in the range   $[0;p)$ , this sequence will eventually converge into a loop. The birthday paradox actually suggests that the expected number of elements is   $O(\sqrt{p})$  until the repetition starts. If   $p$  is smaller than   $\sqrt{n}$ , the repetition will likely start in   $O(\sqrt[4]{n})$ .

Here is a visualization of such a sequence   $\{x_{i}modp\}$  with   $n=2206637$ ,   $p=317$ ,   $x_0=2$  and   $f(x)=x^2+1$ . From the form of the sequence you can see very clearly why the algorithm is called Pollard's   $\rho$  algorithm.

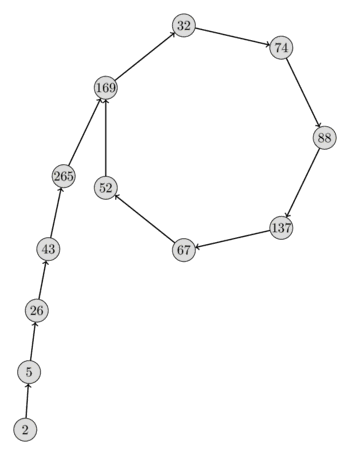
Yet, there is still an open question. How can we exploit the properties of the sequence   $\{x_{i}modp\}$  to our advantage without even knowing the number   $p$  itself?

It's actually quite easy. There is a cycle in the sequence   $\{x_{i}modp{\}}_{i\le j}$  if and only if there are two indices   $s,t\le j$  such that   $x_s\equiv x_{t}modp$ . This equation can be rewritten as   $x_s-x_t\equiv 0modp$  which is the same as   $p|gcd(x_s-x_t,n)$ .

Therefore, if we find two indices   $s$  and   $t$  with   $g=gcd(x_s-x_t,n)>1$ , we have found a cycle and also a factor   $g$  of   $n$ . It is possible that   $g=n$ . In this case we haven't found a proper factor, so we must repeat the algorithm with a different parameter (different starting value   $x_0$ , different constant   $c$  in the polynomial function   $f$ ).

To find the cycle, we can use any common cycle detection algorithm.

Floyd's cycle-finding algorithm

This algorithm finds a cycle by using two pointers moving over the sequence at differing speeds. During each iteration, the first pointer will advance one element over, while the second pointer advances to every other element. Using this idea it is easy to observe that if there is a cycle, at some point the second pointer will come around to meet the first one during the loops. If the cycle length is   $\lambda$  and the   $\mu$  is the first index at which the cycle starts, then the algorithm will run in   $O(\lambda +\mu )$  time.

This algorithm is also known as the Tortoise and Hare algorithm, based on the tale in which a tortoise (the slow pointer) and a hare (the faster pointer) have a race.

It is actually possible to determine the parameter   $\lambda$  and   $\mu$  using this algorithm (also in   $O(\lambda +\mu )$  time and   $O(1)$  space). When a cycle is detected, the algorithm will return 'True'. If the sequence doesn't have a cycle, then the function will loop endlessly. However, using Pollard's Rho Algorithm, this can be prevented.

function floyd(f, x0):
    tortoise = x0
    hare = f(x0)
    while tortoise != hare:
        tortoise = f(tortoise)
        hare = f(f(hare))
    return true

Implementation

First, here is an implementation using the Floyd's cycle-finding algorithm. The algorithm generally runs in   $O(\sqrt[4]{n}\log (n))$  time.

long long mult(long long a, long long b, long long mod) {
    return (__int128)a * b % mod;
}

long long f(long long x, long long c, long long mod) {
    return (mult(x, x, mod) + c) % mod;
}

long long rho(long long n, long long x0=2, long long c=1) {
    long long x = x0;
    long long y = x0;
    long long g = 1;
    while (g == 1) {
        x = f(x, c, n);
        y = f(y, c, n);
        y = f(y, c, n);
        g = gcd(abs(x - y), n);
    }
    return g;
}

The following table shows the values of   $x$  and   $y$  during the algorithm for   $n=2206637$ ,   $x_0=2$  and   $c=1$ .

  $$\begin{array}{|llllll|}\hline i& x_{i}modn& x_{2i}modn& x_{i}mod317& x_{2i}mod317& gcd(x_i-x_{2i},n)\\ 0& 2& 2& 2& 2& -\\ 1& 5& 26& 5& 26& 1\\ 2& 26& 458330& 26& 265& 1\\ 3& 677& 1671573& 43& 32& 1\\ 4& 458330& 641379& 265& 88& 1\\ 5& 1166412& 351937& 169& 67& 1\\ 6& 1671573& 1264682& 32& 169& 1\\ 7& 2193080& 2088470& 74& 74& 317\\ \hline\end{array}$$ 

The implementation uses a function mult, that multiplies two integers   $\le {10}^{18}$  without overflow by using a GCC's type __int128 for 128-bit integer. If GCC is not available, you can using a similar idea as binary exponentiation.

long long mult(long long a, long long b, long long mod) {
    long long result = 0;
    while (b) {
        if (b & 1)
            result = (result + a) % mod;
        a = (a + a) % mod;
        b >>= 1;
    }
    return result;
}

Alternatively you can also implement the Montgomery multiplication.

As stated previously, if   $n$  is composite and the algorithm returns   $n$  as factor, you have to repeat the procedure with different parameters   $x_0$  and   $c$ . E.g. the choice   $x_0=c=1$  will not factor   $25=5\cdot 5$ . The algorithm will return   $25$ . However, the choice   $x_0=1$ ,   $c=2$  will factor it.

Brent's algorithm

Brent implements a similar method to Floyd, using two pointers. The difference being that instead of advancing the pointers by one and two places respectively, they are advanced by powers of two. As soon as   $2^i$  is greater than   $\lambda$  and   $\mu$ , we will find the cycle.

function floyd(f, x0):
    tortoise = x0
    hare = f(x0)
    l = 1
    while tortoise != hare:
        tortoise = hare
        repeat l times:
            hare = f(hare)
            if tortoise == hare:
                return true
        l *= 2
    return true

Brent's algorithm also runs in linear time, but is generally faster than Floyd's, since it uses less evaluations of the function   $f$ .

Implementation

The straightforward implementation of Brent's algorithm can be sped up by omitting the terms   $x_l-x_k$  if   $k<\frac{3\cdot l}{2}$ . In addition, instead of performing the   $gcd$  computation at every step, we multiply the terms and only actually check   $gcd$  every few steps and backtrack if overshot.

long long brent(long long n, long long x0=2, long long c=1) {
    long long x = x0;
    long long g = 1;
    long long q = 1;
    long long xs, y;

    int m = 128;
    int l = 1;
    while (g == 1) {
        y = x;
        for (int i = 1; i < l; i++)
            x = f(x, c, n);
        int k = 0;
        while (k < l && g == 1) {
            xs = x;
            for (int i = 0; i < m && i < l - k; i++) {
                x = f(x, c, n);
                q = mult(q, abs(y - x), n);
            }
            g = gcd(q, n);
            k += m;
        }
        l *= 2;
    }
    if (g == n) {
        do {
            xs = f(xs, c, n);
            g = gcd(abs(xs - y), n);
        } while (g == 1);
    }
    return g;
}

The combination of a trial division for small prime numbers together with Brent's version of Pollard's rho algorithm makes a very powerful factorization algorithm.

Practice Problems

• SPOJ - FACT0
• SPOJ - FACT1
• SPOJ - FACT2
• GCPC 15 - Divisions

Contributors:
• jakobkogler (85.05%)
• chloeimb (9.81%)
• adamant-pwn (3.51%)
• 0xGodspeed (0.7%)
• pokorj54 (0.47%)
• jxu (0.23%)
• kyomukyomupurin (0.23%)